[TS] CH05. 확률과정 실습

Time Series
Author

김보람

Published

October 31, 2023

해당 자료는 전북대학교 이영미 교수님 2023고급시계열분석 자료임

import

library(forecast)
getwd()
'/home/coco/Dropbox/coco/posts/1. Class/Time Series' 
options(repr.plot.width = 12, repr.plot.height = 6)

정상시계열

z <- rnorm(200) #z~normal(0,1)

\(\{ z_t, t=1,2,\dots, \}, n=200\)

먼저 시도표를 그리자.

ACF/PACF도 중요해!

  • ACF: \(\rho_1 = Corr(Z_t, Z_{t+1}) \rightarrow \hat \rho_1 = \dfrac{\hat \gamma_1}{\hat \gamma_0}\)

\(\hat \gamma_0 = \dfrac{1}{n} \sum_{i=1}^n (Z_t - \bar Z)^2\) : Var임

\(\hat \gamma_1 = \dfrac{1}{n} \sum_{t=1}^{n-1} (Z_t - \bar Z)(Z_{t+1} - \bar Z) \rightarrow(Z_1-\bar Z)(Z_2-\bar Z) \dots (Z_{n-1} - \bar Z)(Z_n - \bar Z)\)

(a <- c(1,2,3))
  1. 1
  2. 2
  3. 3
data.table::shift(a,2)
  1. <NA>
  2. <NA>
  3. 1

2만큼 이동

cor(z, data.table::shift(z,1))
<NA>
  • data.table에 있는 shift함수: 위에서는 z를 1만큼 shift시키라는 함수
cor(z, data.table::shift(z,1), use = 'pairwise.complete.obs')
0.0806503414196885
  • 옵션을 줘야 오류가 안난다. NA를 빼고 cor을 구해주라는 옵션
plot.ts(z, lwd=2)
abline(h=0, lty=2)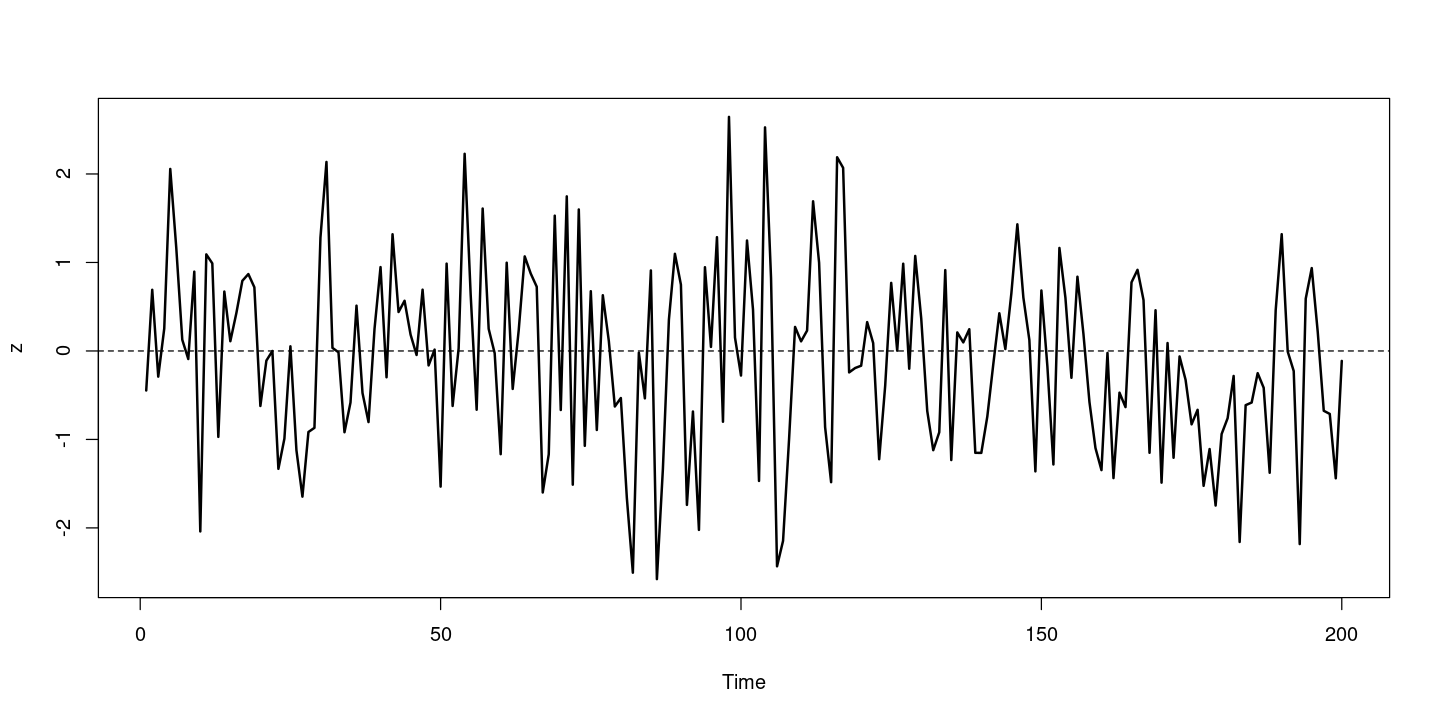

  • 평균이 0을 중심으로 되어있고, 등분산성으로 보인다.
par(mfrow=c(1,2))
acf(z, ylim=c(-1,1),lag.max=24)
pacf(z, ylim=c(-1,1),lag.max=24)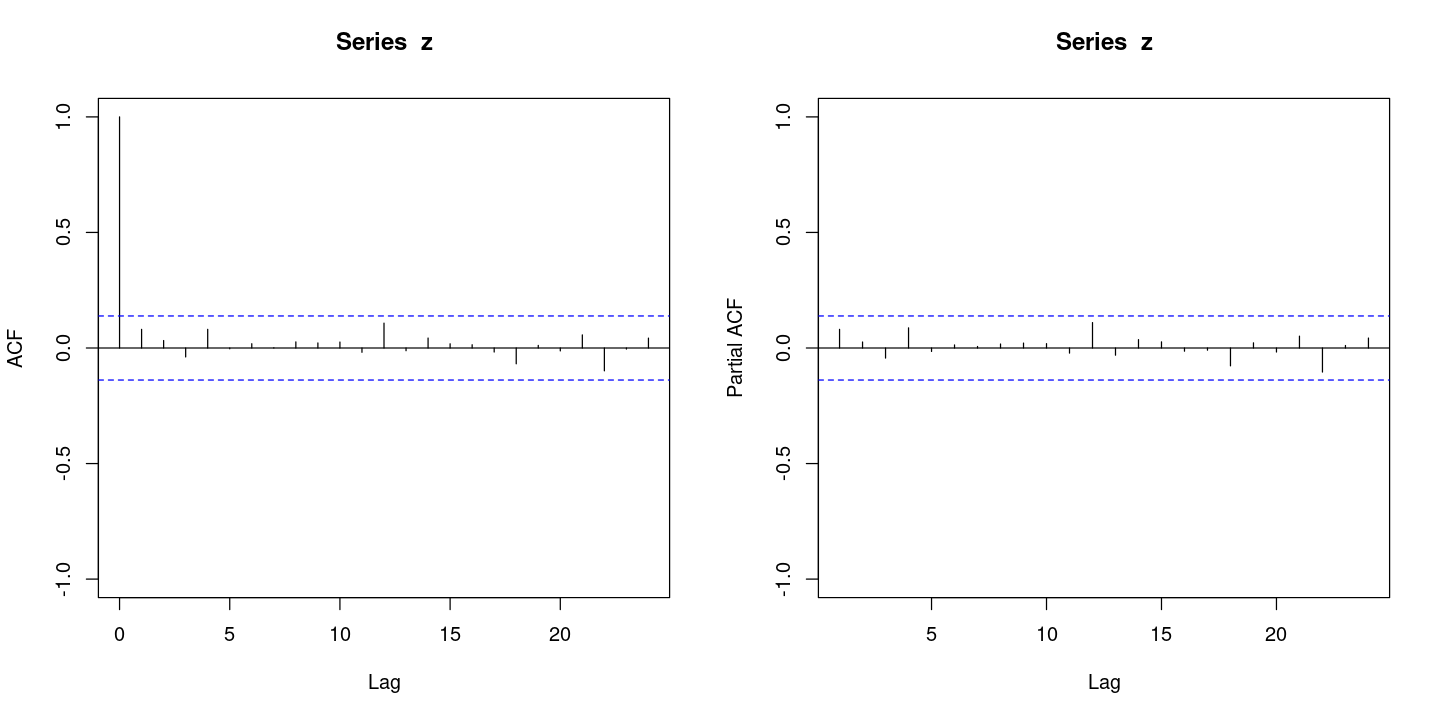

  • lag.max=24인것은 주기로 생각해서 24를 많이 하는데 변경 가능하다

  • ACF: 시차 사이의 corr

  • PACF: 중간 사이의 효과를 뺀 corr

  • 파란색 점선: 기각역, 그 안에 있으면 통계적으로 유의하지 않다! 다 0이다.

  • \(\rho_1\)는 시차가 0이니까 자기자신은 항상 0

  • 왼쪽 그림에 2번째 \(\rho\)값은 위에서 구한 0.0806503414196885 값이고, 이는 오른쪽 그림에서 첫번째 선값과 동일

layout(matrix(c(1,1,2,3), 2, 2, byrow = TRUE))
plot.ts(z,col='steelblue',
main = paste0(' iid N(0,1)'))
abline(h=0, col='grey', lty=2)
acf(z)
pacf(z)
graphics.off()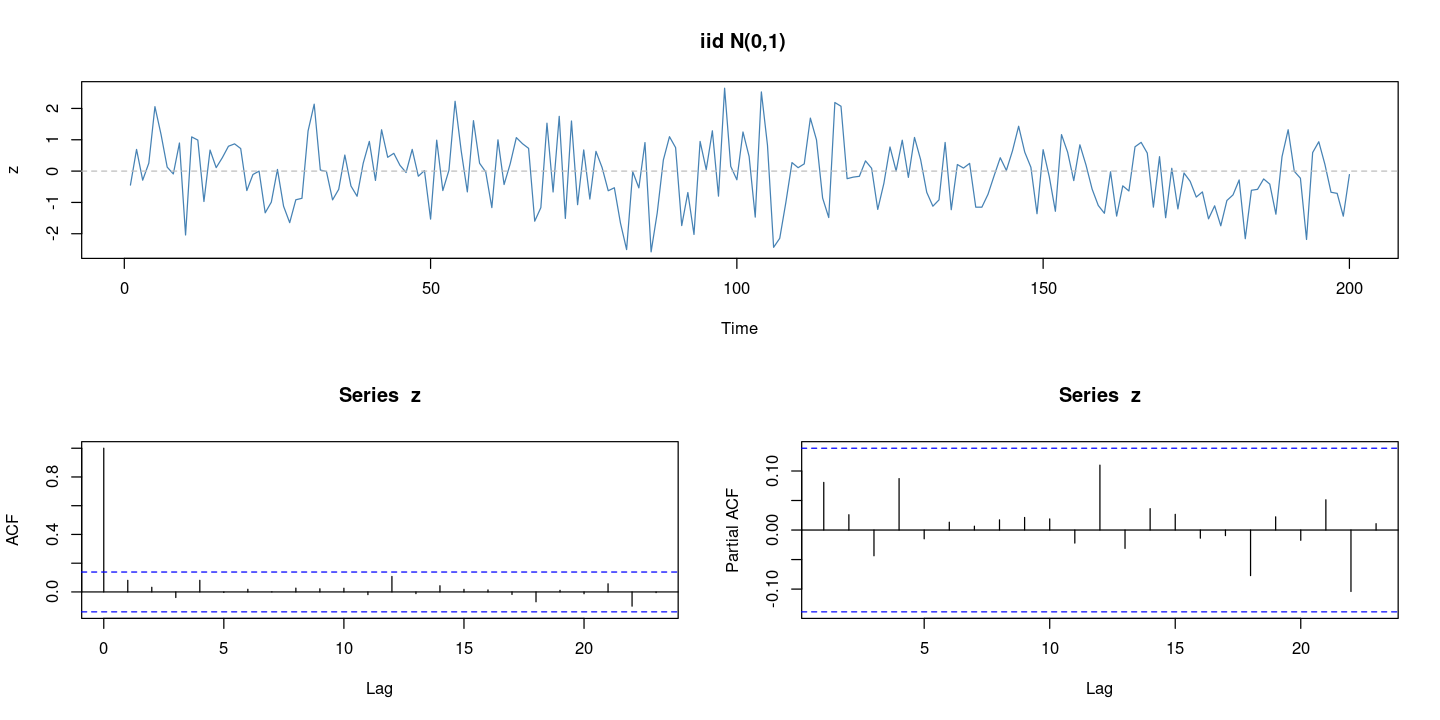

  • 백색잡음이다.
forecast::tsdisplay(z)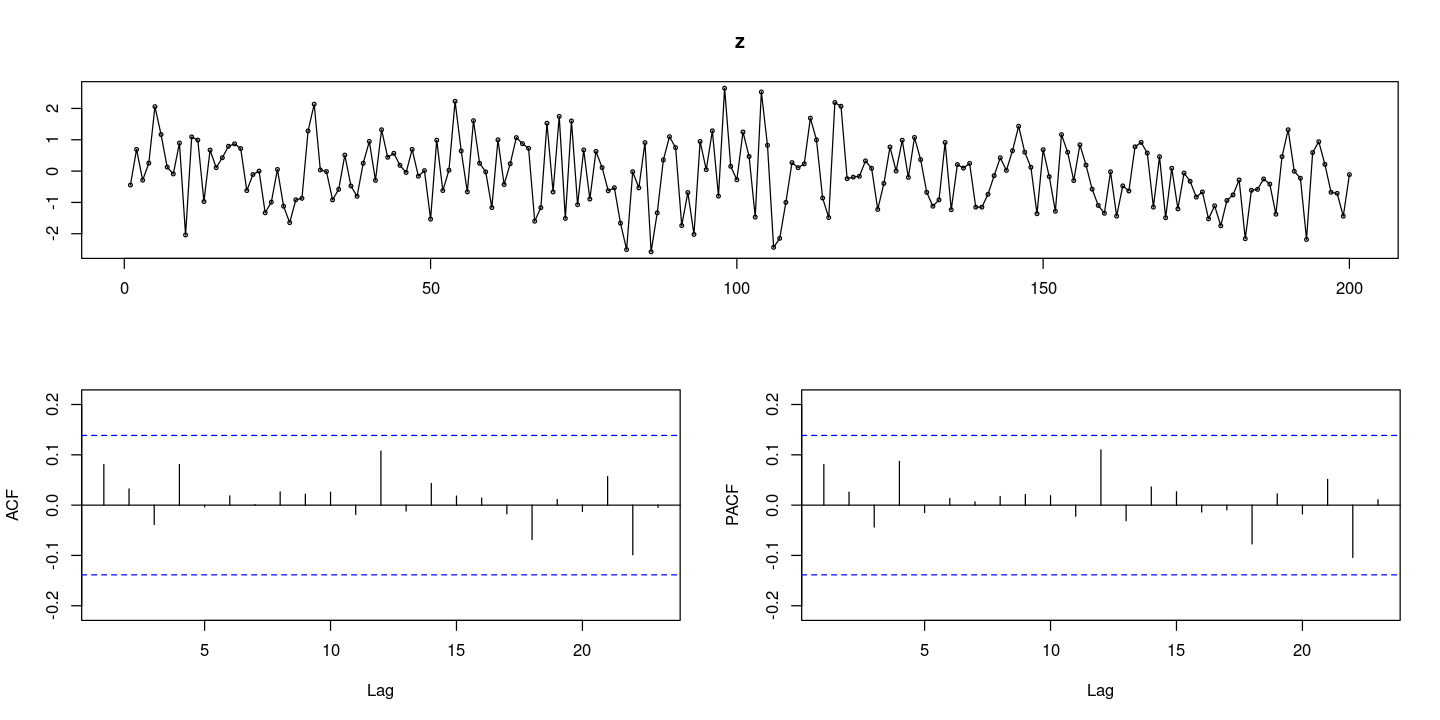

forecast::ggtsdisplay(z)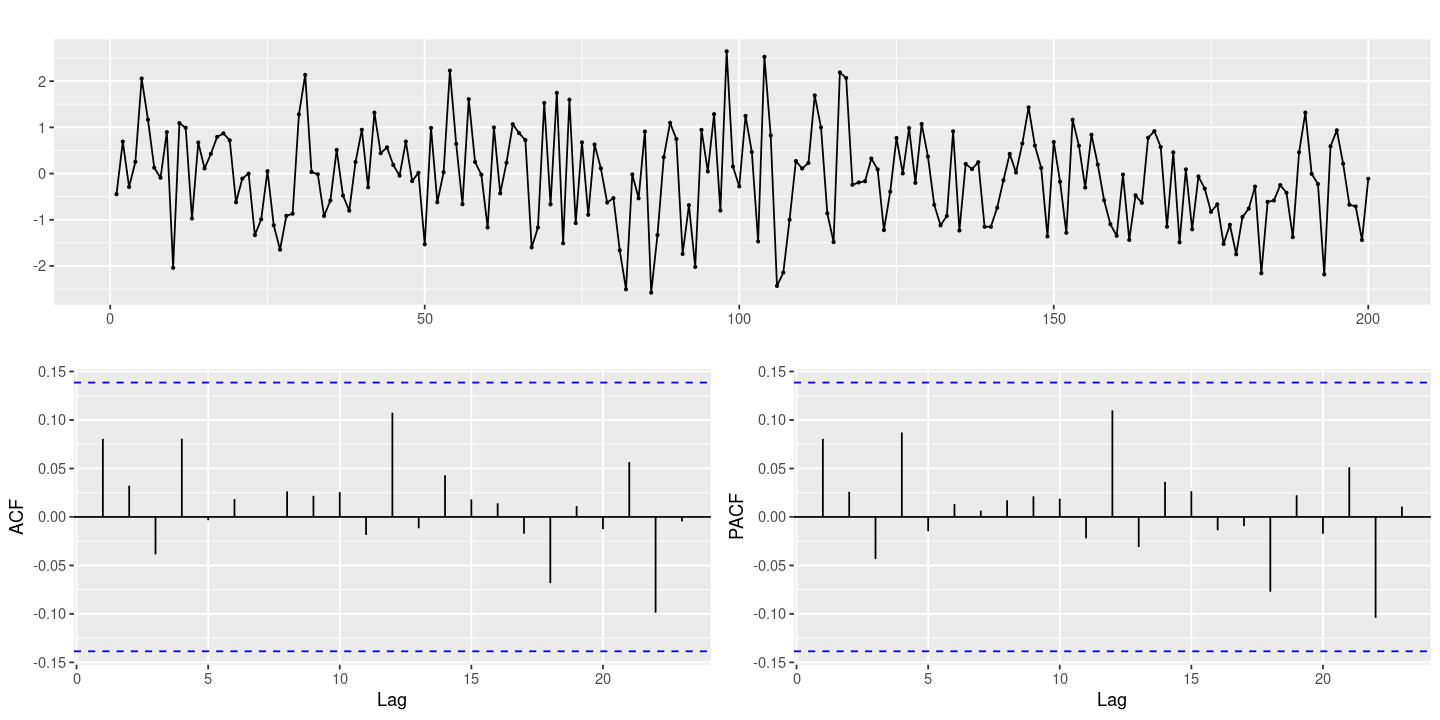

확률보행과정

\(Z_t = Z_{t−1} + ϵ_t = ϵ_1 + ϵ_2 +⋯+ ϵ_t, ϵ ∼ WN(0, σ^2)\)

\(Z_1 = \epsilon_1\)

\(Z_2 = \epsilon_1 + \epsilon_2\)

각각의 오차들을 더해나가는거..

(a <- 1:4)
cumsum(a)
  1. 1
  2. 2
  3. 3
  4. 4
  1. 1
  2. 3
  3. 6
  4. 10

- cumsum: 누적합

z = rnorm(200, 0, 1)
rw = cumsum(z)
plot.ts(rw,)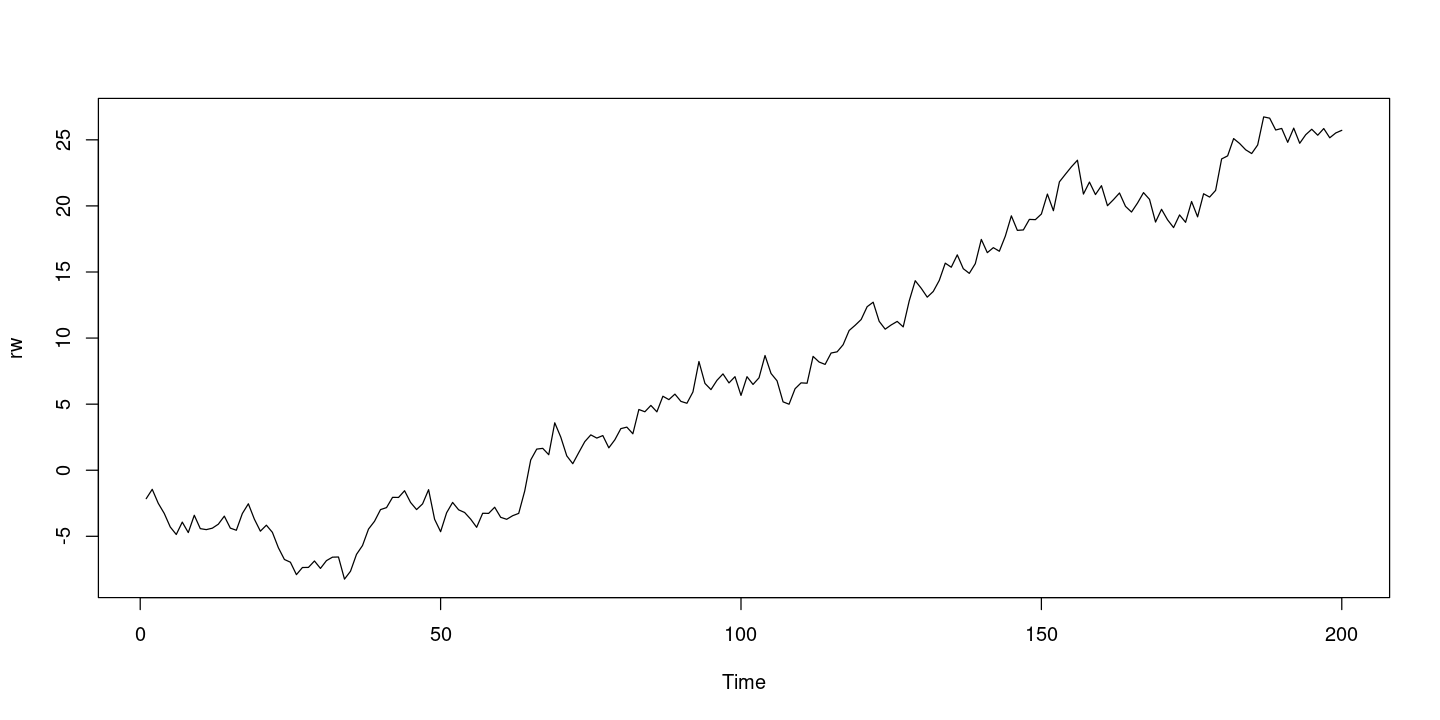

  • 랜덤워크는 형태가 계속 변한다.ㅡ
z = rnorm(200, 0, 1)
rw = cumsum(z)
forecast::tsdisplay(rw,
main = "Random Walk Process")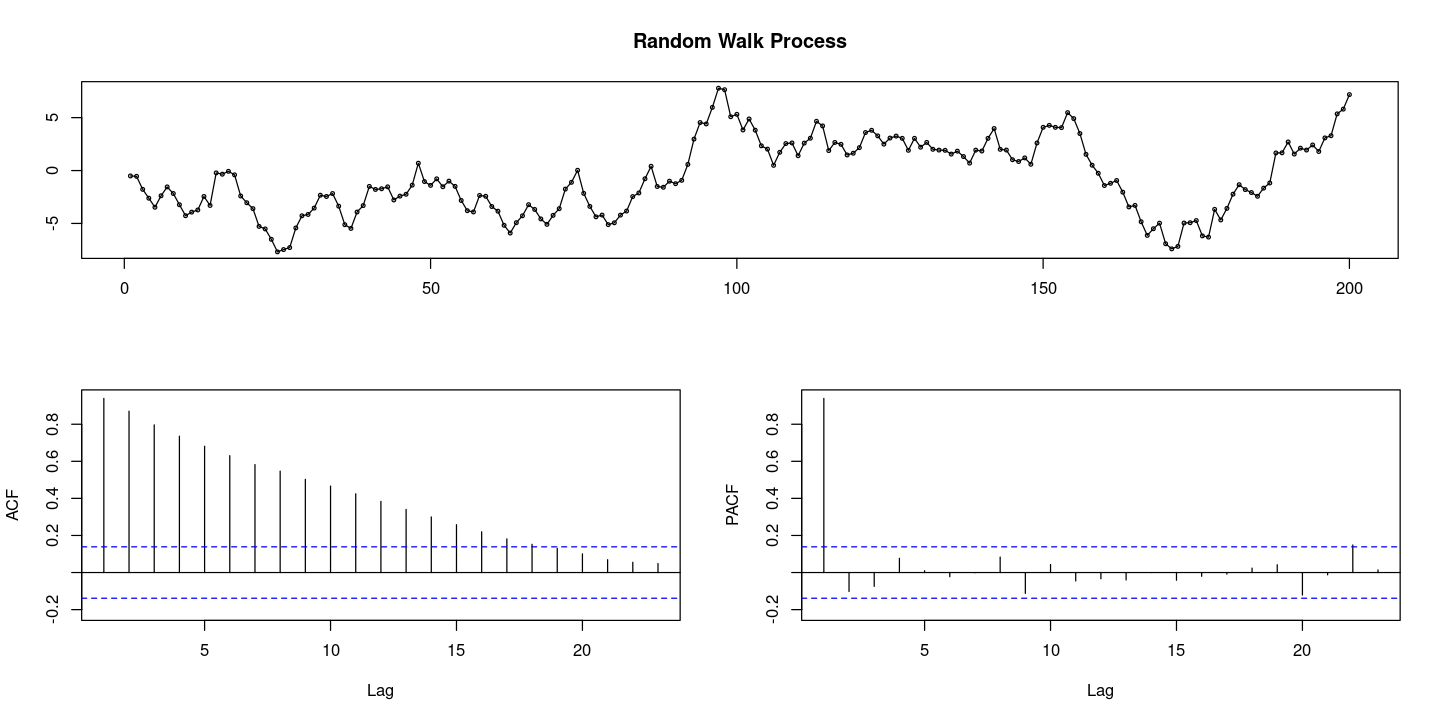

  • ACF가 빨리 감소하나 천천히 감소하냐를 확인하자.

- 확률적 추세: 추세가 있는 것 같기도 하고.. 바뀌는 것 같기도 하고.. ACF가 천천히 감소하면 확률적 추세가 있구나 라고 생각

  • \(Z_t = Z_{t-1} + \epsilon_t= \epsilon_1 + \epsilon_2 + \dots + \epsilon_t\): 현재 오차나 과거 오차가 다 영향을 주고 있다.

  • \(Z_t - Z_{t-1} = \epsilon_t\): 차분하면 WN이 된다.

- 결정적 추세: 눈에 보이는

- 차분 관련 함수

diff_rw = diff(rw,1)

forecast::tsdisplay(diff_rw)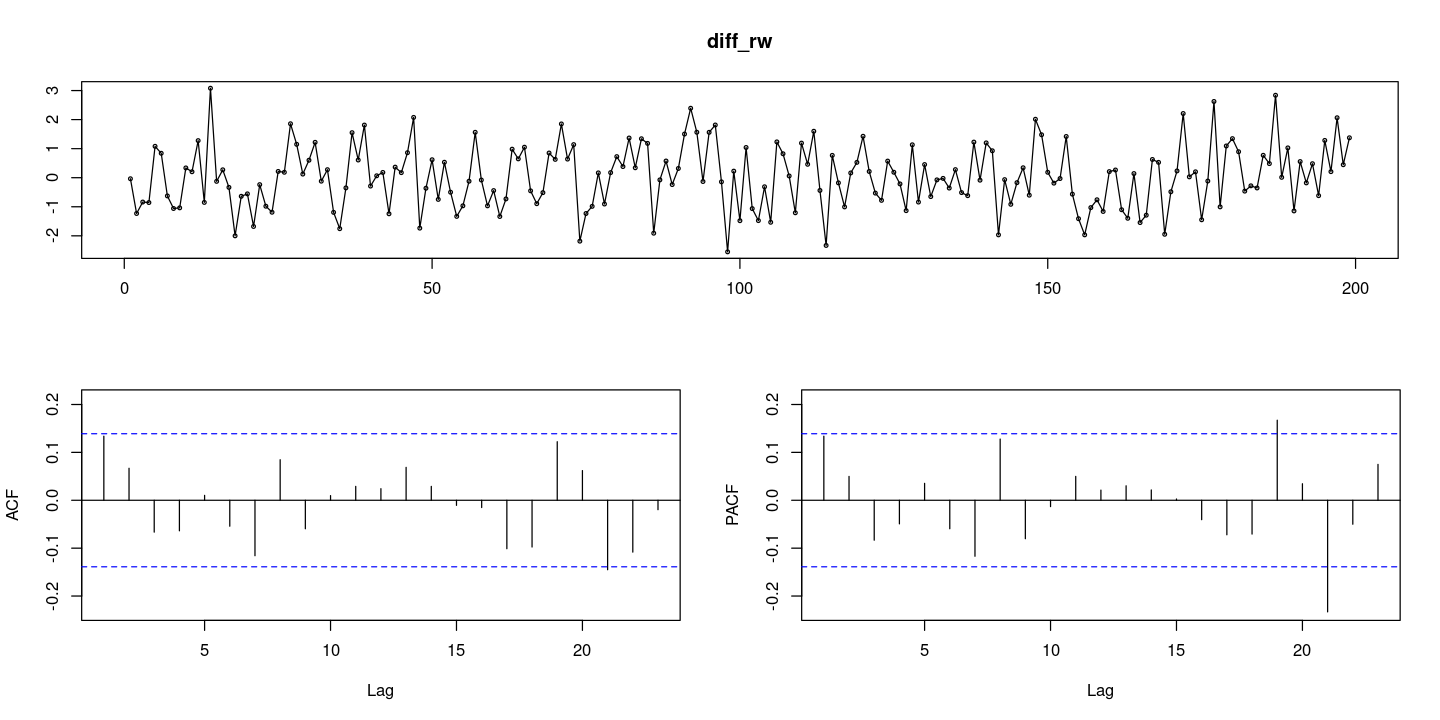

절편이 있는 확률보행 과정

\(Z_t = δ + Z_{t−1} + ϵ_t = tδ + ϵ_1 + ϵ_2 +⋯+ ϵ_t, ϵ ∼ WN(0, σ^2)\)

rw_wd <- c()
delta <- 0.3
rw_wd[1] <- delta + rnorm(1)
for(k in 2:200){
rw_wd[k] <- delta + rw_wd[k-1] + rnorm(1)
}
plot.ts(rw_wd)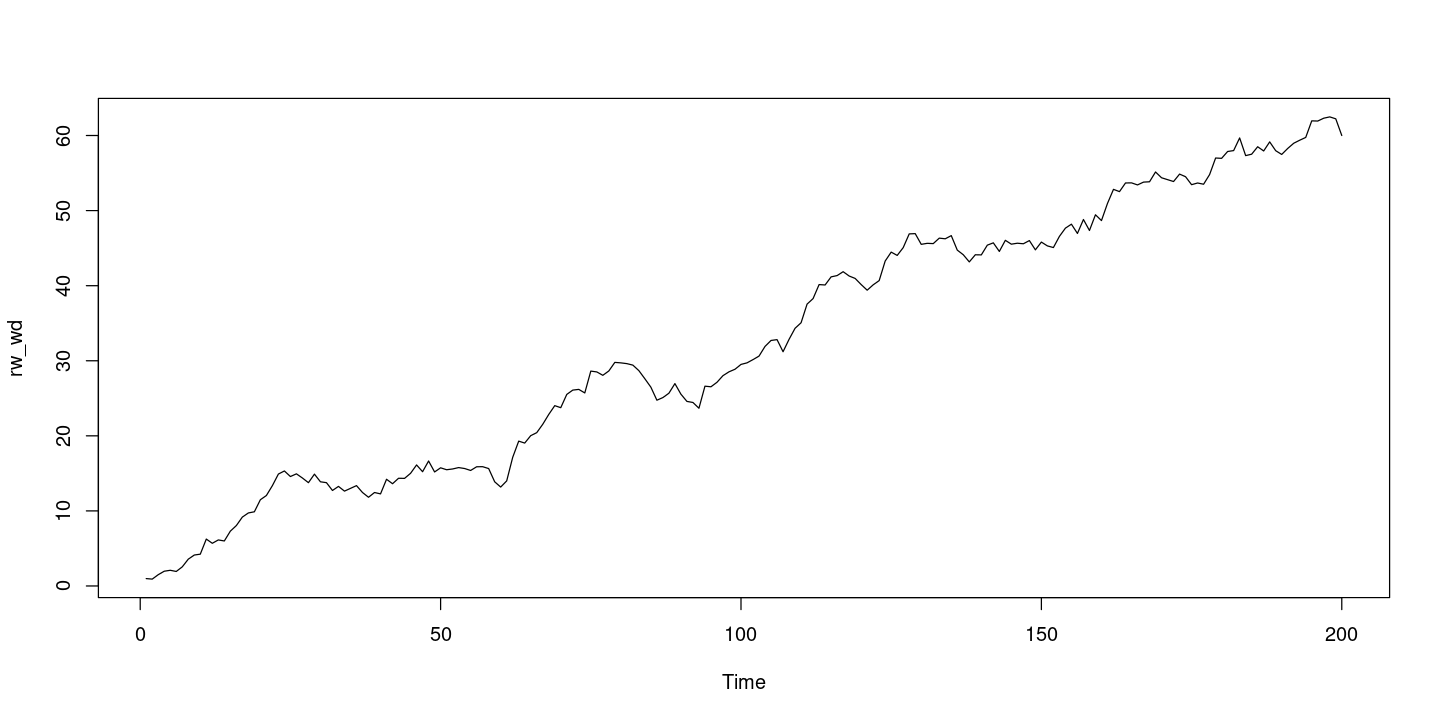

- 위와 똑같은 함수

n <- 200
rw_wd <- (1:n)* delta + cumsum(rnorm(n))
forecast::tsdisplay(rw_wd,
        main = "Random Walk Process with Drift")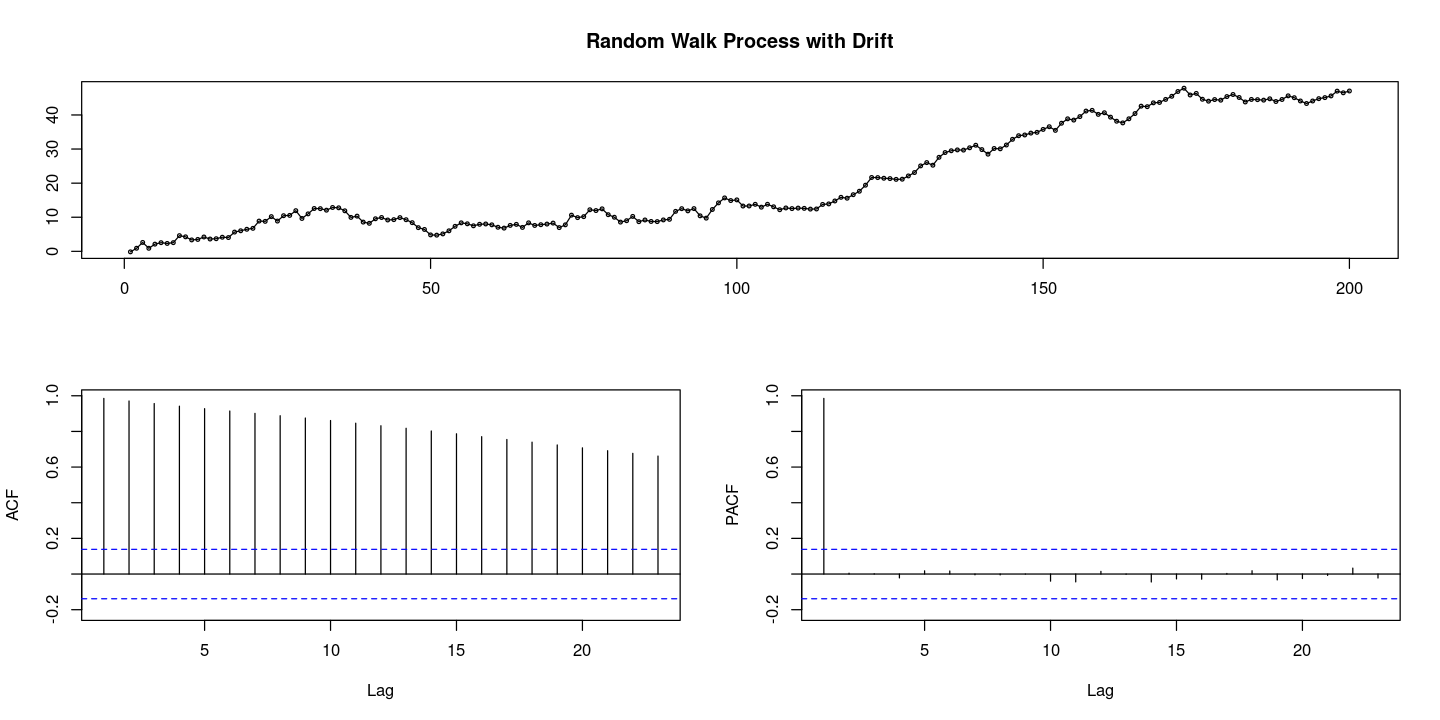

  • 확률적 추세가 있다.

여러가지 데이터에 대한 ACF PACF

sin

t <- 1:100
z <- sin(t*pi/3) #주기6
plot.ts(z)
points(t,z, pch=16)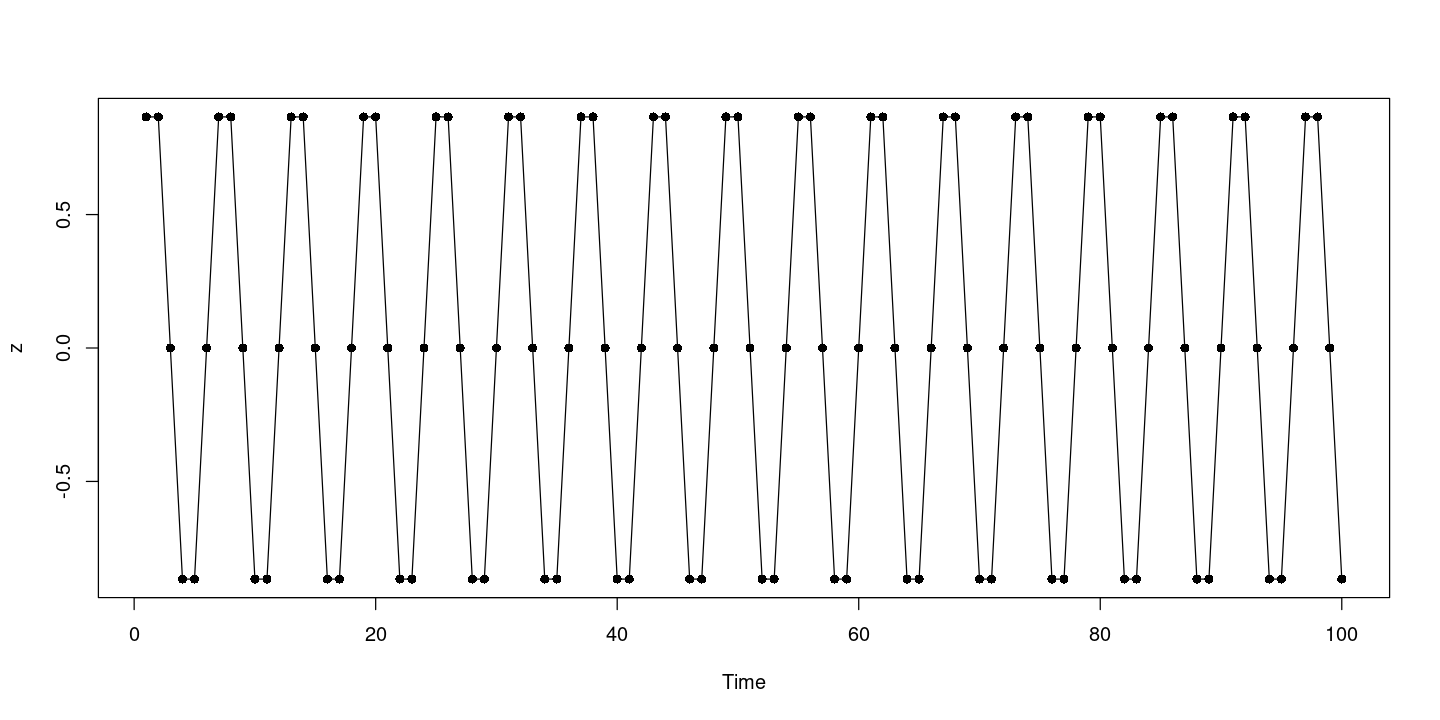

forecast::tsdisplay(z)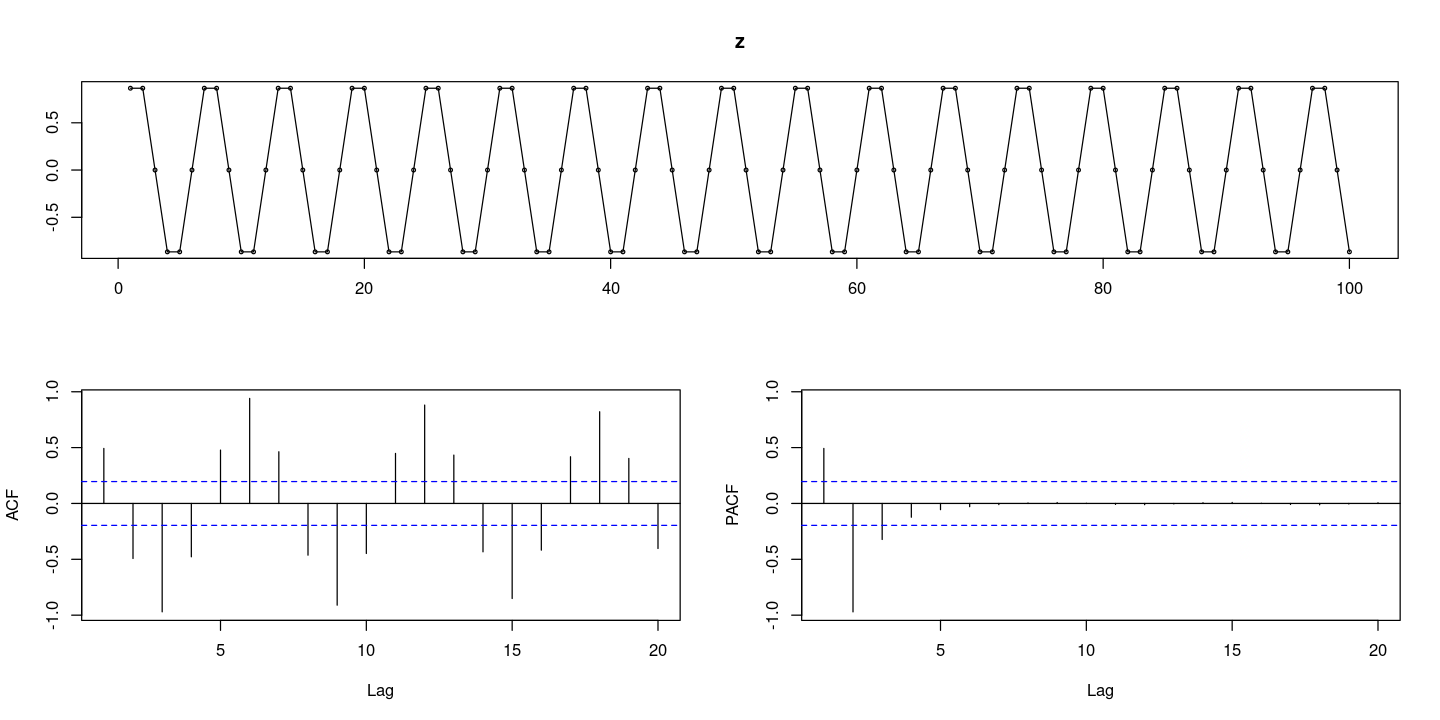

  • 주기가 6인게 좀 튀어나와있음
s <- 12
z <- sin(2*t*pi/s) + rnorm(100,0,0.4)
forecast::tsdisplay(z)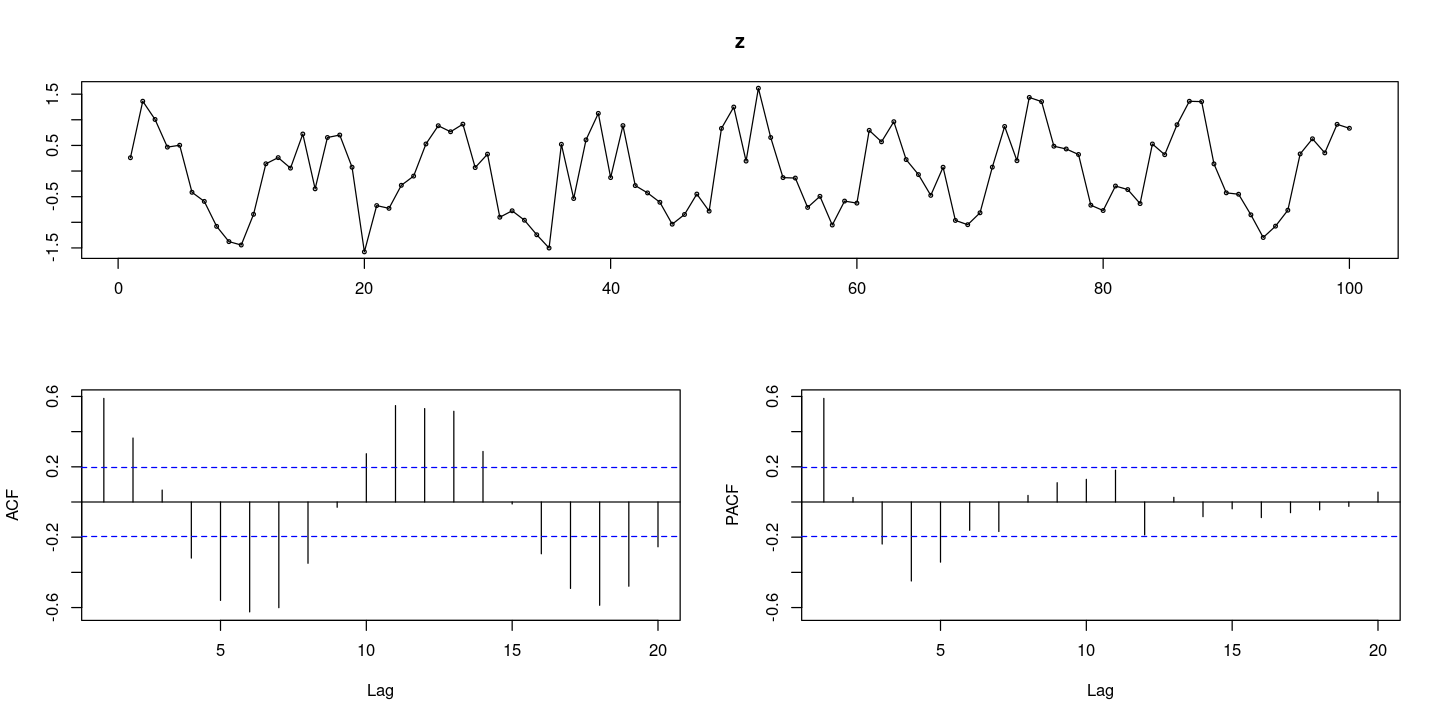

  • 오차있고 주기가 12인거
s <- 12
z <- 0.2*t + 2*sin(2*t*pi/s) + rnorm(100,0,1.2)
forecast::tsdisplay(z)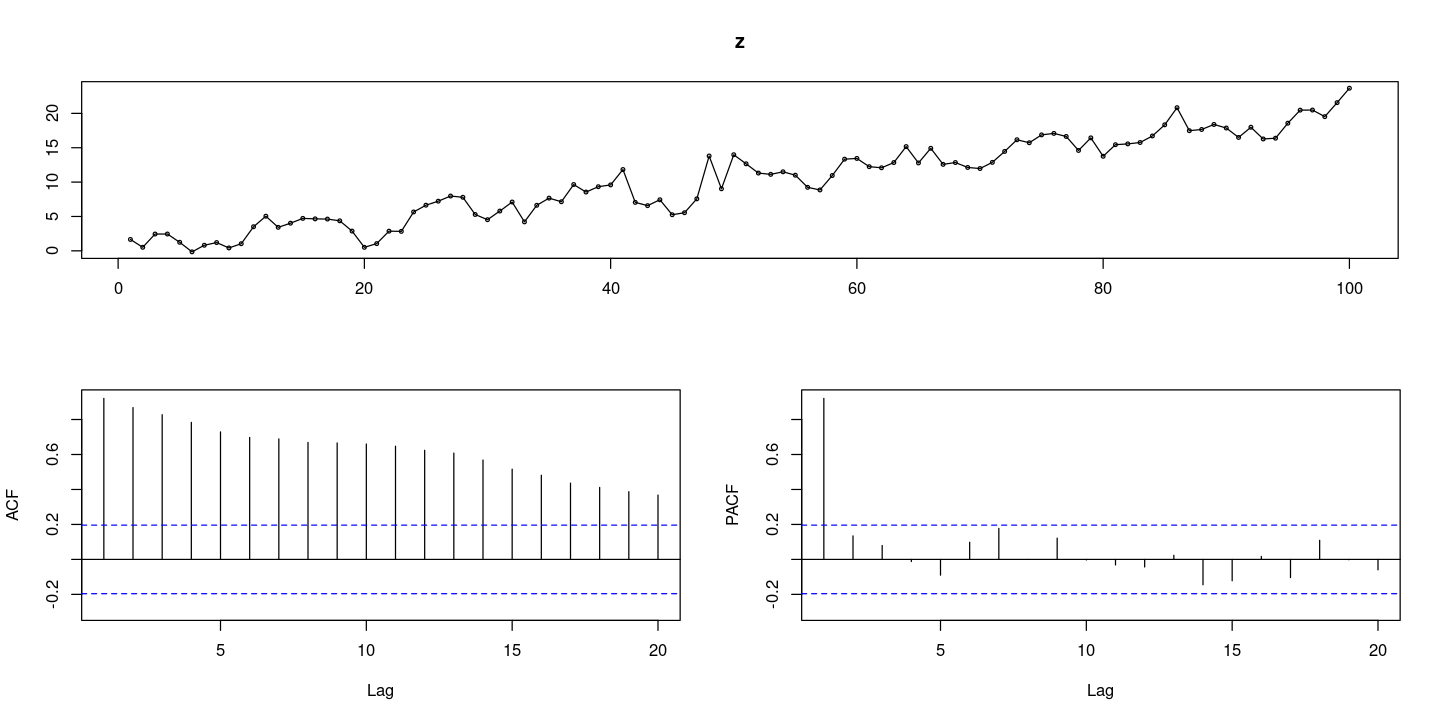

  • 천천히 감소하다가 중간에 튀어나온게있음(계절성분때문에)

population

z <- scan("population.txt")
forecast::tsdisplay(z)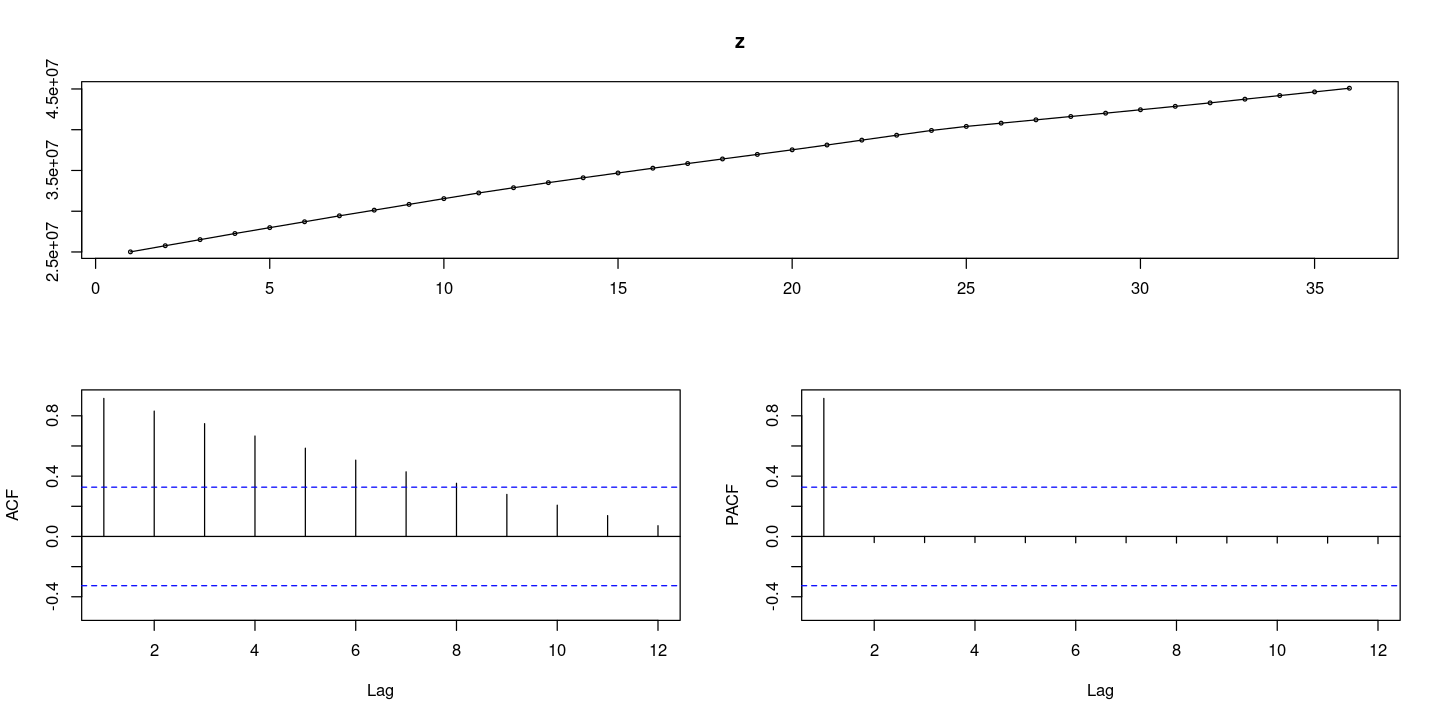

  • 선형 추세: ACF가 천천히 감소하고, PACF는 1차시만..

depart

z <-scan("depart.txt")
forecast::tsdisplay(z, lag.max=60)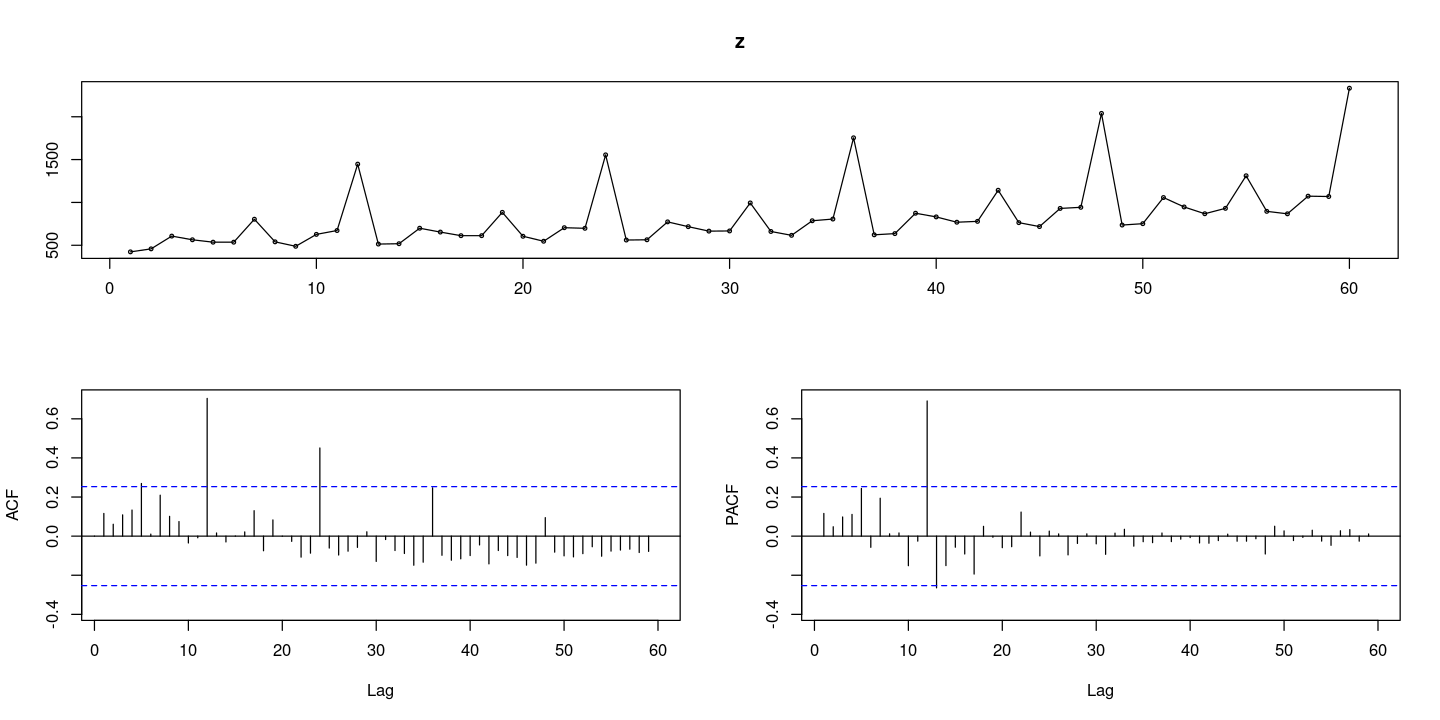

  • 계절성분 있고, 추세는 거의 없다.

  • 추세가 있다면 acf가 감소함

  • 튀어나오는 부분-> 계절성분 때문에

  • ACF는 12,24,36,48,60 에서 튀어나오는데 갈수록 적게 튀어나옴.. -> 계절주기가 12이면 12,24,36이 비슷한 영향?? 이라 생각할 수 있어.

  • PACF는 12,36을 알면.. 오차만 남으니까 24만 튀어나옴. 24만 유의미해.

mindex

z <- scan("mindex.txt")
forecast::tsdisplay(z)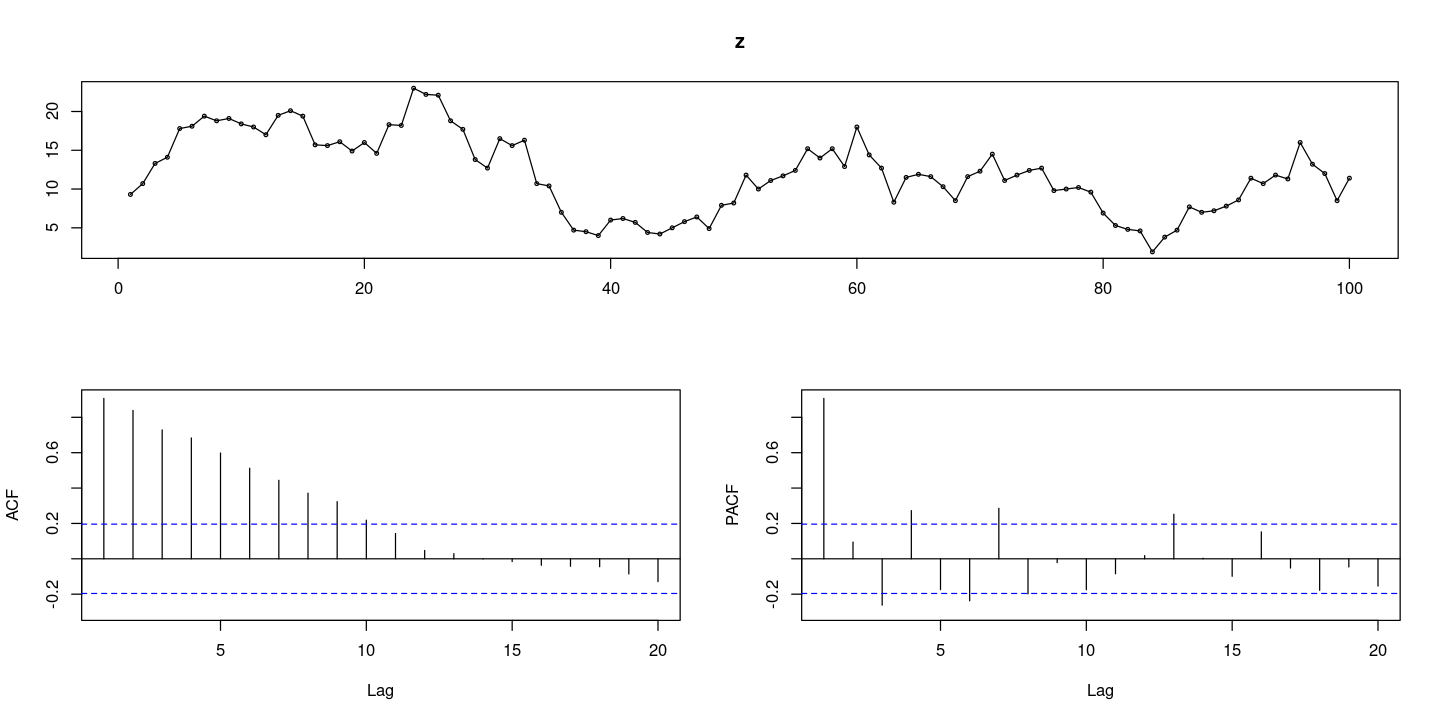

  • PACF에서 조금 튀어나오는 건.. 무시..

stock

z <- scan("stock.txt")
forecast::tsdisplay(z)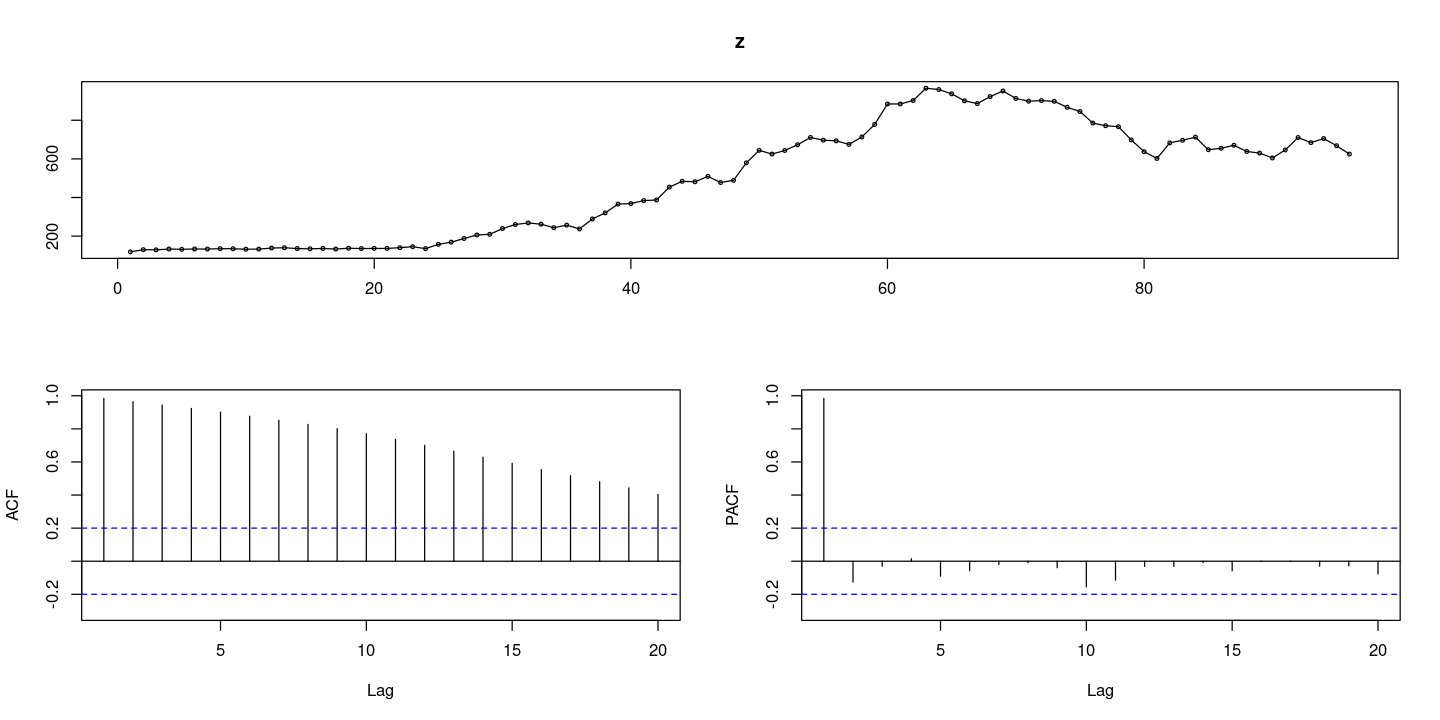

  • 추세가 있으니 ACF가 천천히 줄어들고, PACF가 첫번째만 살고 나머지는 다 0

koreapass

z <- scan("koreapass.txt")
forecast::tsdisplay(z)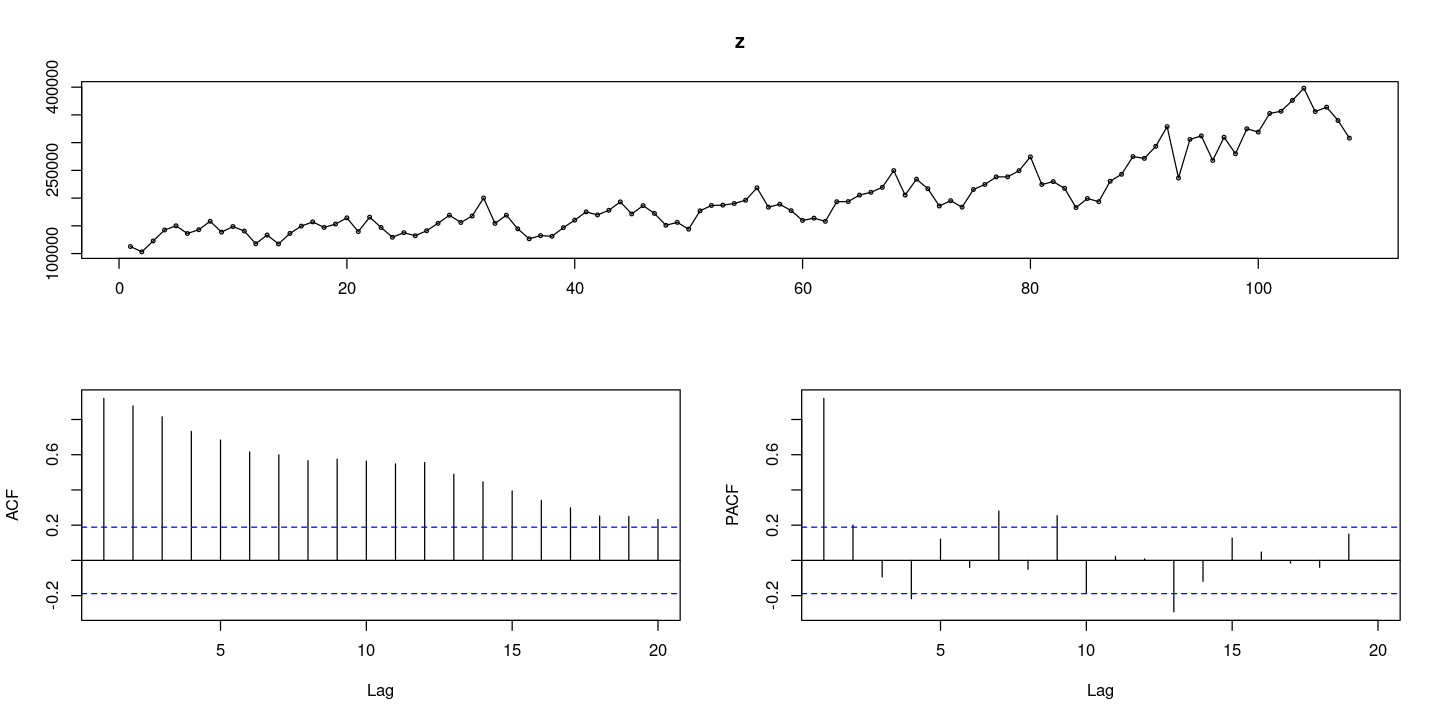

  • 이분산성이 있으니 로그변환을 하자
logz <- log(z)
forecast::tsdisplay(logz)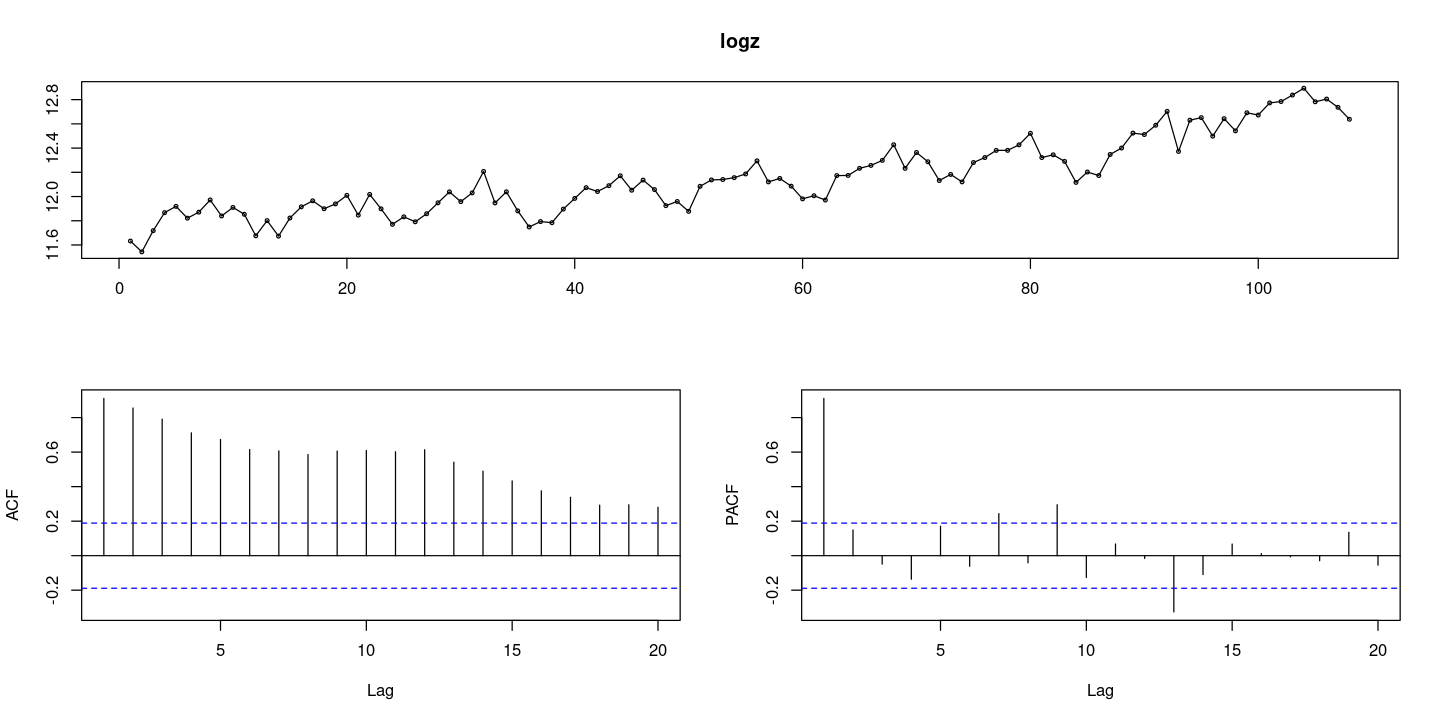

  • 시도표는 변하지만 ACF랑 PACF는 변하지 않아. 로그변환한거랑은 상관없다
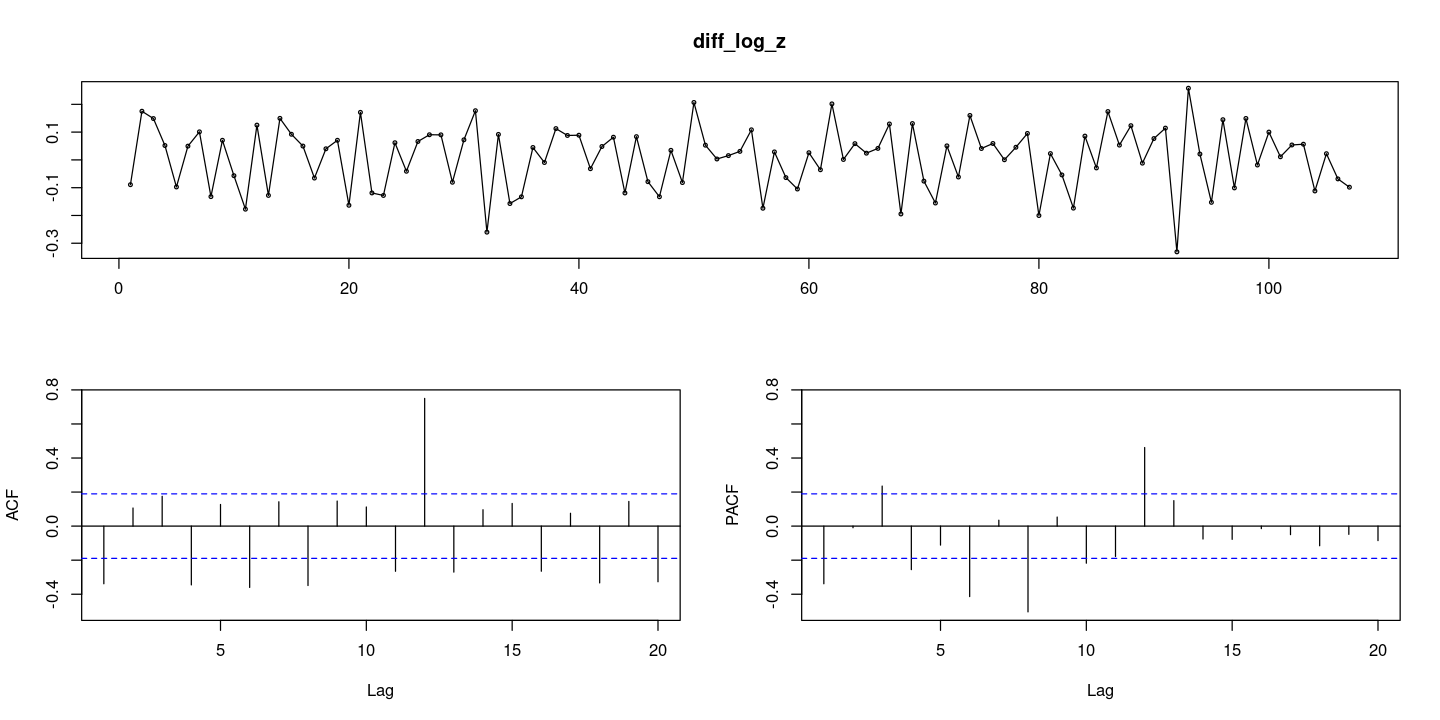
diff_log_z <- diff(log(z))
forecast::tsdisplay(diff_log_z)